Growth-System
My research into L-Systems gave me a lot of results directed towards cellular and fractal structures constructed recursively using a simple set of rules. This alone produces uniform, unnatural vegetation. To simulate the diverse variation in real plants, other factors must interfere with the fractal properties. Streit (Federl and Sousa) suggested an algorithm to take pre-existing plant models and warped them based upon gravity and plant stimuli. e.g. light, local plant life.
I required an algorithm capable not of physically accurate growth, but generating visually pleasing vegetation that could react to an environment. I took the concepts of gravity, stimuli and recursion, creating a simple growth algorithm based upon weights to produce a reactionary plant structure. I began experimenting with constraints to shape the plant around the scene in order to produce vine type structure.
My initial attempts to expand branches from nodes resulted in some visually acceptable results. The vines would creep along floors and drape over edges, the results appeared natural. For each node I created a growth direction based upon several weights; sun direction, gravity, previous growth direction. I cast a ray in that direction and any resultant collision information was used to ensure the direction did not intersect the scene. However, the algorithm became fairly unstable in geometrically complex areas. Vines would exhaust space and intersect the scene, continuing to growing downwards due to gravity. The ray-casting method was just too unstable.
In searching for a solution to the algorithms instabilities, I discovered an ivy generation implementation capable of creeping ivy over a mesh surface. The author (Luft), used a much simpler, more robust approach. Rather than attempting to repel growth, nodes were attracted to a surface based upon distance. I implemented a similar approach, brute force testing against all triangles to find the closest point on a surface, and then clamping the new child node to this surface. The results were far more stable and produced good results even across a larger scale.
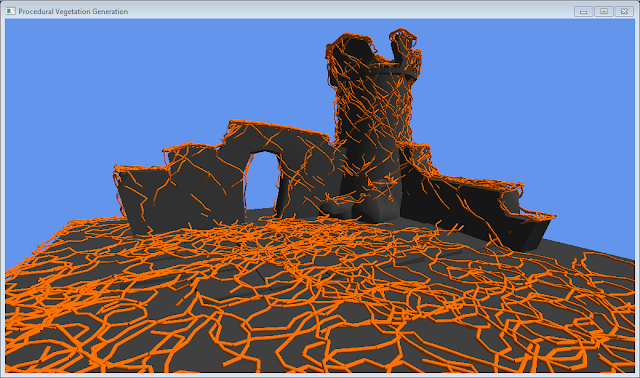 |
| Ray-casting Method |
 |
| Surface Attraction Method |
Real-time Updates
As the system is designed for testing control over the procedural algorithms, I decided to migrate the growth system to a real-time solution. The growth is performed in small iterations, allowing the updated node database to be redrawn each frame. This should provide faster and higher quality feedback when testing controls for the growth system.
An interesting bug also arose when moving to a real-time update system, a snapshot of the database had to be taken before each growth step to prevent concurrent iteration and manipulation. This forced each node to be searched within the real database and caused an explosion of branches when two nodes had the same position. This problem would occur particularly on mesh corners, where nodes would be constrained to exactly the same position.
For now the bug is fixed by merging matching nodes to remove any duplicates. However, perhaps running the growth system on a separate thread would alleviate both the bug and much of the overhead incurred with copying and searching within the database upon each growth iteration.
Distribution Culling
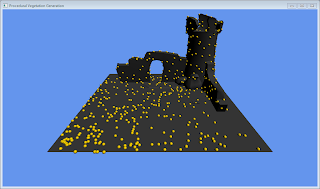
I earlier in the project development I suggested culling the distributed nodes by firing a hemisphere of rays into the scene to find an occlusion value. I implemented this concept and found the distribution patterns to be quite useful. As vines and other vegetation is likely to grow out of cracks and crevices in the ground, I constrained the distribution height and fired 16 rays from a possible node location into the scene to find the occlusion value.
The results are a natural spread of nodes around the wall and tower, good for interesting vines growth over the scene.
Performance
While performance is fairly acceptable on small scenes with few polygons, it does not scale well to larger more complex scenes. Both ray-cast occlusion culling and closest surface point algorithms rely on brute force iteration through all the scene triangles. As these are the current application bottlenecks, both these algorithms will need improvement to attain higher performance.
References
Streit, L.; Federl, P.; Sousa, M.C. "Modelling Plant Variation Through Growth". 2005
Computer Graphics Forum. Volume 24, Issue 3, pp. 497-506.
Blackwell Publishing, Inc.
Luft, T. An Ivy Generator. 2007
A tool to interactively model three-dimensional ivys.
http://graphics.uni-konstanz.de/~luft/ivy_generator/
[Accessed 17/01/2012]