Raycasting
I wrote a raycasting algorithm to allow rays to be fired at a mesh and return information about the closest collision. Although I am not currently using it for distribution, I believe this can be used for a variety of purposes when attempting to cull distributed points. I could fire a ray towards the sun to check if a plant would have sunlight, or fire multiple rays in a hemisphere to find corners and crevices for plants to grow in.
Point Distribution
I worked mostly on implementing a high quality point distribution algorithm to position points across the scene. I plan to use these points to provide initial spacial data from which plants can grow.
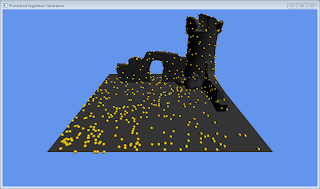
First the mesh is analysed and a list of triangle weightings are built, the weighting is dependent entirely upon area. I then distribute points across each triangle dependent upon the weighting and distance from other nodes. Once a node position is computed it is added into the node database, and a debugging render of the database is displayed.
My first attempt suffered from some ugly artefacts. The point density was lost on small triangles due to the triangle area being too small to add any points. You can see in the image above, much of the tower has no point coverage. Clamping the density to a minimum of 1.0 gave smaller triangles excessive point density. The solution was simply to accumulate the area from each triangle, allowing several smaller triangles to accumulate a point density (right).
 |
| Rand() |
 |
| Mersenne Twister |
 |
| Rand() - Poisson Disk |
I decided to try and force the points apart by implementing a Poisson Disk algorithm with the distribution. For each point I performed a brute force distance comparison against all other points in the node database. Only if the point is outside the radius of all other points can it be added to the database. To maintain the desired density, the algorithm will continuously attempt to add points until a maximum iteration count is met. The results on the left are much better, with points very evenly spread across the plane.
 |
| Rand() - Poisson Disk(Low Density) |
 |
| Rand() - (Turk, 1995) |
The final algorithm gives controllable high quality non-uniform results, allowing for a minimum distance between points. Resultant nodes are stored in the database with correct positioning and normals.
Performance
I was interesting in investigating the scalability and performance of the algorithm as any user control would become very cumbersome to use if the algorithm became a large stall in the application. I was unsure how well the algorithm would handle larger scenes, because point radius check required a brute force O(n^2) number of of comparisons against all other nodes in the node database. I applied the algorithm to a much large scene (as seen below) and profiled the application.
The results were as expected, the application initially hung for a large period of time while processing the scene and the profiler results showed that the majority of time was spent performing distance comparisons in the node database.
I decided to redesign the node database in order to improve performance. I implemented a spacial hashing algorithm based upon Hastings (Mesit and Guha, 2005) . Each new node's position is hashed and indexed into an ordered multi-map. As I do not need to concern myself with volumes, the hashing becomes extremely simple and fast. After implementing the new node database I re-profiled the same scenario, and found the results to be very surprising. Not only did the algorithm increase vastly in performance, the algorithm bottleneck has now become the random number generation. The cost of finding a local node has become negligible.
References
Bedaux, J. "C++ Mersenne Twister Pseudo-Random Number Generator" 2003
http://www.bedaux.net/mtrand/
[Accessed 12/01/2012]
Hastings, E.; Mesit, J.; Guha, R. "Optimization of Rendering, Collision and AI Routines in Large-Scale, Real-Time Simulations by Spatial Hashing".
Summer Computer Simulation Conference 2005, USA
M. Matsumoto and T. Nishimura,
Mersenne Twister: A 623-Dimensionally Equidistributed
Uniform Pseudo-Random Number Generator,
ACM Transactions on Modeling and Computer Simulation,
Vol. 8, No. 1, January 1998, pp. 3-30
http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/emt.html.
Tulleken, H. "Poisson Disk Sampling". 2009
Dev.Mag Issue 21, released in March 2008
http://devmag.org.za/2009/05/03/poisson-disk-sampling/
[Accessed 17/01/2012]
Turk, G. "Generating Random Points In Triangles"
Graphics Gems, 1995, pp. 24-28
Xerox Palo Alto Research Center, Palo Alto, Californi.